Engineering a chess match against my brother

This is the story of me trying to win a game of chess against my brother. A single freaking game. What’s so special about it? Am I good at chess? Not at all. Did I improve at my game in the process? Also no. Is it a story about “the journey rather than the destination”? Not really. Did I at least have fun in the process? Not so sure. This is the story of me trying to be unconventional at probably the most studied game in existence and using my software engineering background for something that probably doesn’t need it.

Although I’m a total disaster at chess and this post is useless to whoever seriously wants to improve at their game, I still think it was worth sharing how it’s possible to apply software engineering principles to a problem. Was I successful? You’ll see at the end.

Intro: why I got into chess

During the 2020 COVID19 pandemic, my brother, along with many other people, took a passion for playing online chess. After playing for a couple of months he started speaking very enthusiastically about it and challenging other family members, but where my father would budge (and get digitally butchered) I wouldn’t. For one thing, I refrained myself from delving into a potentially very time consuming hobby. I knew enough about chess to understand that to become even a mediocre amateur club player you’d still need to sink hundreds if not thousands of hours in the game. I admit I also didn’t like the thought of losing against my brother, which was certain at the time, since he already had hundreds of games under his belt and I had none.

One day I finally gave in and accepted a challenge from him. Needless to say that I lost completely. I knew the rules and the rudimentary of the game, having played a little bit as a kid, but my brother was obviously no match. Looking at the post-game analysis in chess.com I saw that my disadvantage only grew, move by move, until reaching a +9 evaluation (equivalent to having lost one rook, a bishop and a pawn to zero), which is beyond any hope for a comeback, where I resigned. This blueprint was followed during another couple of matches, where I understood I had to do something to avoid being demolished every time.

This was when I decided I wanted to study the game a bit more.

First attempt: learn

My first attempt in trying to improve at the game was to do the obvious: head to Reddit and YouTube to see what other learners recommended. Between a tutorial from GM Naroditsky, some reading and puzzle solving on Lichess, I also played a few games with random people on the Internet. My rating stayed pretty low nevertheless (1300 - 1400 Rapid on Lichess).

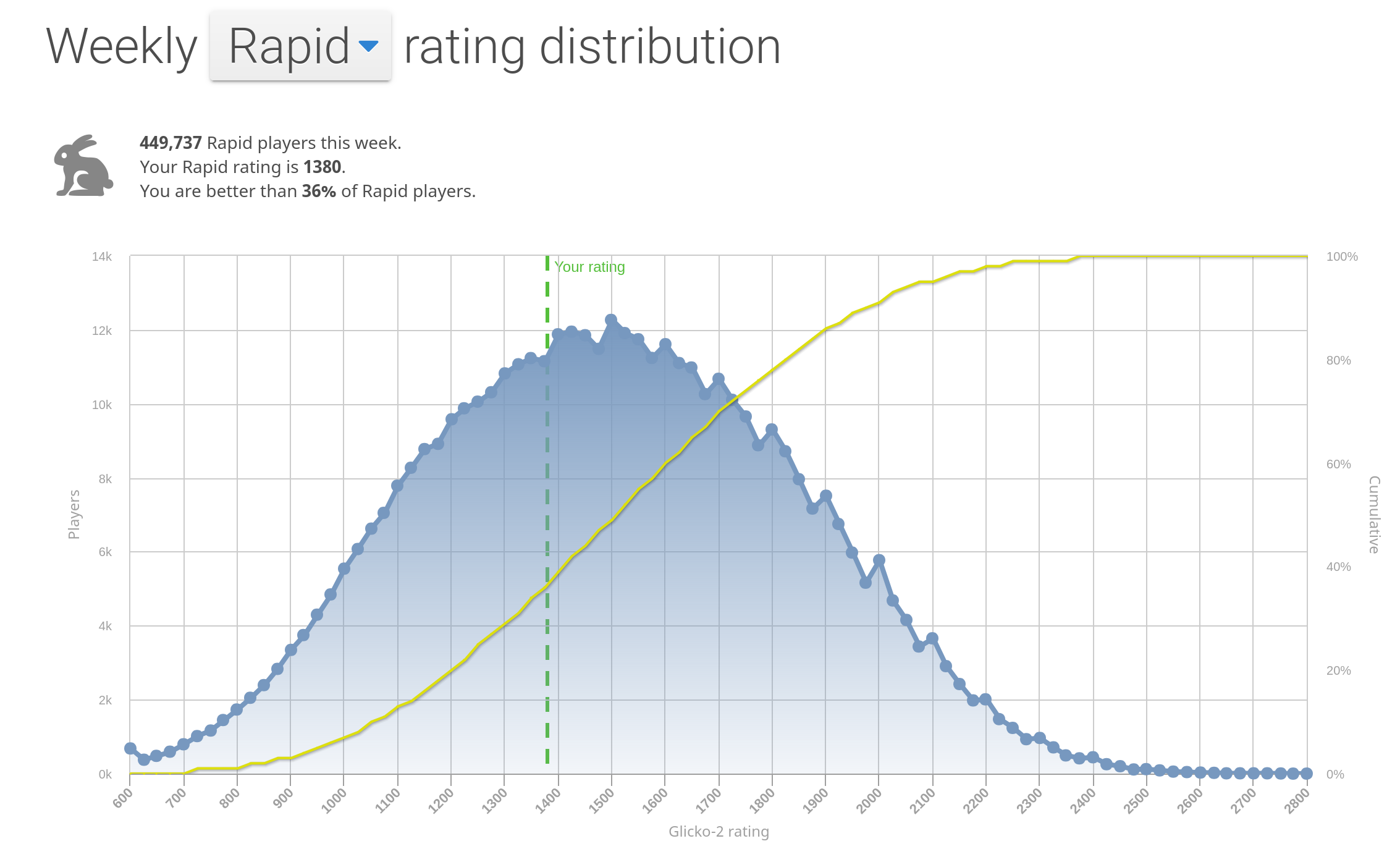
After another couple of lost matches against my brother, it dawned on me that I had no hope of beating him. I was following his same steps to improve (playing, studying the game, watching videos), but I was dedicating much less time. At that point he was playing hundreds of games a month and I was willing to play maybe 10. At that pace I was only going to get further and further behind.

It was at that point that I had my second realization: I didn’t really care about the game, I didn’t want to really improve at chess in general, I only cared about beating a single person: my brother.

Second attempt: study the opponent

A chess match can be generally divided into three phases: the opening, the middlegame and the endgame. Converting a significant advantage into a victory during an endgame is usually “easy”, after studying some basic checkmate patterns, so the question for me was how to get that advantage in the first place. Gaining advantage during a middlegame is usually achieved by long-term strategy and tactics. The first can be improved by reading and studying the game principles (something I can enjoy) while the second is only possible by doing puzzles (which I don’t particularly like doing). I knew that I would be at a disadvantage here, given that my brother used to do about 20 puzzles a day on chess.com, something I would never be able to catch up to. This only left one possibility: gaining advantage during the opening.

Chess opening theory is humongous and involves memorizing long sequences and variations of moves, along with possible replies from the opponent. Beginners don’t really need to memorize much, but some familiarity with the most common openings can go a long way (or so I was told). What I tried then was to look at some random games that my brother played and try to study the openings he was using. I looked at the Italian opening and Sicilian defense on Lichess and tried to memorize the basic ideas behind them. I also watched a bunch of videos on YouTube.

Obviously my brother had already done all of this before me (and better) and so I understandably lost again. Not to mention that memorizing meaningless (at least to me) opening moves is boring and laborious. I didn’t really have fun doing any of that. Another issue was that after my opponent deviated from the known book moves, I had no idea about how to react, because I didn’t really understand the positions.

It was time to step back and think again. I realized then I wasn’t really trying to beat my brother, but I was trying to improve my game against opponents that played his same openings perfectly. Could I be more specific? Could I prepare against my brother’s weaknesses instead? Obviously this wouldn’t work against any player other than him, but that still satisfied my goal.

Third attempt: engineering

The problem to solve became: find positions out of the opening that my brother (PlayerX from now on, for simplicity) would likely reach and be at a disadvantage. Remember that neither of us is an expert of the game and at our level players don’t play very accurately. The only way to play against a good player would be to follow book moves accurately, because you at least know in advance there’s no move they can make to gain an advantage. The story is different when you play against a club player. You can take risks (i.e. be temporarily at a disadvantage) if you know that your opponent is unlikely to be able to find the correct response and so get into trouble.

I also had a list of over 500 games my brother played on chess.com. Being a software engineer, it came natural to me to approach this as any other engineering problem.

I started by downloading the games he played by using the chess.com APIs and split them between black and white games. I focused on the games he played as black, given that I felt I had better chances at guiding the game where I wanted if I played as white.

import json
import requests

def get_month_games(player, yyyy_mm):
    url = 'https://api.chess.com/pub/player/{}/games/{}'
    r = requests.get(url.format(player, yyyy_mm))
    if not r.ok:
        raise Exception('get_month_games failed')
    games = json.loads(r.content)
    # Format: {games: [{url, pgn}, ...]}
    return games['games']

# ...

import chess.pgn
import io
import json

with open('games.json') as f:
    data = json.load(f)

games = []
for game in data:
    pgn = io.StringIO(game)
    games.append(chess.pgn.read_game(pgn))

black_games = [g for g in games if g.headers["Black"] == "playerx"]

Then I formulated the problem in this way: “Given all the positions PlayerX has seen, what are the ones that he’s likely to reach out of the opening where he is at a substantial disadvantage?”.

Now I had a well formulated problem and I was finally playing in a domain I was familiar with. I decided to do my analysis in Python and in particular to use a Jupyter notebook, because I didn’t really want to create a reusable tool, but only to explore the available data and find one solution. It turns out Python already has pretty amazing libraries to manipulate chess games: python-chess (moves generation, validation, visualization) and python stockfish (bindings to evaluate a chess position by using the famous Stockfish chess engine).

I translated the problem into a graph problem in this way: A node is a particular chess position (described in FEN notation). An edge links two nodes where the destination is reachable from the source position by doing a valid move. There’s a special initial node that is common to all games: the initial position.

I then constructed the graph of all games played by PlayerX as black, additionally annotating every edge with the number of times the particular move was played.

class GamesGraph():
    def __init__(self):
        self.graph = igraph.Graph(directed=True)

    def add_move(self, start_fen, end_fen, uci):
        vs = self._ensure_vertex(start_fen)
        vt = self._ensure_vertex(end_fen)
        try:
            e = self.graph.es.find(_source=vs.index, _target=vt.index)
            e["count"] += 1
        except:
            e = self.graph.add_edge(vs, vt)
            e["uci"] = uci
            e["count"] = 1

    @property
    def start_node(self):
        return self.graph.vs.find(chess.STARTING_FEN)

    def _ensure_vertex(self, fen):
        try:
            return self.graph.vs.find(fen)
        except:
            v = self.graph.add_vertex(name=fen)
            v["fen"] = fen
            v["turn"] = chess.Board(fen).turn
            return v

What results is weighted directed graph (not a tree because a position can be reached with different sequences of moves) similar to this one (a synthetic one because the real one would be too big to fit here):

Here the initial position is the squared node, the color indicates whether from that position it’s black or white’s turn.

I also wanted an evaluation of each position in terms of advantage for white and to do so I used Stockfish. Given that the process of evaluating thousands of positions is somewhat time consuming, I decided to do that separately and create a JSON object mapping each unique FEN position to its Stockfish evaluation.

from stockfish import Stockfish

stock = Stockfish(parameters={"Threads": 8})
stock.set_depth(20)
stock.set_skill_level(20)

def eval_pos(fen):
    stock.set_fen_position(fen)
    return stock.get_evaluation()

# fens is a map between a FEN string and a node of the graph.
for fen, node in graph.fens.items():
    node.eva = eval_pos(fen)

The evaluation is returned in centipawn advantage or “mate-in X moves”, where a positive number means advantage for white and negative is an advantage for black:

{"type":"cp", "value":12}    # 12 centipawns advantage for white.
{"type":"mate", "value":-3}  # Black has mate in three.

100 centipawns represent the advantage of having one more pawn than your opponent and 300 is a minor piece like a bishop. Note however that Stockfish assigns a value to pieces depending on their position, so it’s entirely possible to have an advantage of 1000 even if the pieces on the board are equal.

I needed to map this evaluation into something more manageable, like a number between 0 and 1. To do so, I decided arbitrarily that an advantage of 300+ is mapped to 1.0 and a disadvantage of 300+ is mapped to 0. Additionally, any mate in X (even if X is 20) is 1 or 0.

# Returns [-1;1]
def rating(ev, fen):
    val = ev["value"]
    if ev["type"] == "cp":
        # Clamp to -300, +300. Winning a piece is enough.
        val = max(-300, min(300, val))
        return val / 300.0
    # Mate in X: also max rating.
    if val > 0: return 1.0
    if val < 0: return -1.0
    # This is already mate, but is it for white or black?
    b = chess.Board(fen)
    return 1.0 if b.turn == chess.WHITE else -1.0

# Returns [0;1], where 0 is min, 1 is max advantage for black.
def rating_black(ev, fen):
    return -rating(ev, fen) * 0.5 + 0.5

The information was then all there, I just needed to find nodes in the graph (i.e. positions) where black was at a disadvantage, along with the sequence of moves that was most likely to reach it. I needed to weigh the edges in such a way that it was possible to easily compute the probability to reach a certain position. My reasoning was as follow:

• At every position, we can evaluate the probability of doing a certain move by dividing the number of times the corresponding edge was taken by the total number of moves done from that position.
• Every edge will now have a weight between 0 and 1, where the higher the number, the higher the probability the edge will be taken from that position.
• The probability of a certain path is then the product of the probability of all the traversed edges.

To solve the problem with standard graph algorithms I needed to transform the weights at the edges in such a way that:

• They represent a distance instead of a probability (i.e. the longer the distance, the lower the probability of the path).
• The distance between two nodes is the sum of the weights of the traversed edges (as opposed to the product of probabilities).

This is actually easier to do than to explain. The actual formula is very simple:

distance(e) = -log(prob(e))

Or, in Python:

def compute_edges_weight(vertex):
    all_count = sum(map(lambda x: x["count"], vertex.out_edges()))
    for edge in vertex.out_edges():
        prob = edge["count"] / all_count
        edge["prob"] = prob
        edge["weight"] = -math.log(prob)

Taking the logarithm of the probability of an edge will give a negative number, because the probability is between 0 and 1. We don’t have to worry about the case of probability zero (which would shoot the logarithm to minus infinity), as every edge of the graph has been taken at least once. The lower the probability, the more negative the logarithm will be, so inverting its sign will make it satisfy our requirements, because:

• The sum of logarithms is the same as the logarithm of the product of their arguments: log(a) + log(b) = log(a*b).
• The bigger the result, the lower the underlying probability.

Equipped with this data, we can compute the shortest path between the initial node and all other nodes by using Dijkstra’s algorithm. The result is a mapping between every node and the shortest path to the initial position, which represents the sequence of moves most likely to land in that position.

At that point I arbitrarily chose a minimum advantage and sorted the paths by probability. The first few paths represented my best chances to gain an advantage out of the opening against PlayerX.

Tweaks

What did I find? This was a position returned by the algorithm above (white to move):

As you can see the situation for black is pretty bad (+8.9 according to Stockfish), because g6, the last move for black, was a mistake. White will go on, take the e5 pawn and the rook. The game for black is pretty much over, as they scramble to save the knight, the h7 pawn and the bishop. Another result was this one (white to move):

Which is mate in one move (Scholar’s mate).

The problem here is that these were mistakes done several times by PlayerX only during his first matches and never repeated again. Early queen attacks are usually carried out by very inexperienced players and they are effective only against players at that level. PlayerX hasn’t fallen for that trap for a long time afterwards, because better opponents don’t play that kind of move! I knew that I couldn’t really use this opening, because PlayerX knew how to defend against it now and would not fall for it anymore.

Another problem was related to sequences of moves that happened only once, but coming from common positions. The probability of the final position was the same as the probability of the last common position, because every edge had a probability of 1.0 (given that no other possibilities have been played). In the example below (edges marked with their probabilities), you can follow the edges with 7 and 6 (the most common position at move 2), but then follow one of the edges with a 1. From that point on, all the subsequent moves will have been played only once (because only a single match reached that position) and so every step will have a probability of 1.0.

And this is how the probabilities look like:

This is intuitively incorrect, as it’s improbable that the same exact sequence of moves will be played with absolute certainty. We don’t have enough games being played from those positions to know that.

The famous quote (from Brewster?) “In theory there is no difference between theory and practice, while in practice there is”, was true in this case as well, so I needed a few tweaks and manual inspection to find better candidate positions.

To correct the second problem I decided to put an upper bound to the probability of an edge, so long sequences of moves played only once will gradually lose probability.

def compute_edges_weight(vertex, prob_ceiling=0.9):
    all_count = sum(map(lambda x: x["count"], vertex.out_edges()))
    for edge in vertex.out_edges():
        # Certainty doesn't exist... Let's put a probability ceiling (default 90%).
        prob = min(edge["count"] / all_count, prob_ceiling)
        edge["prob"] = prob
        edge["weight"] = -math.log(prob)

For the first problem I just manually screened out bad suggestions. At the end of the day I only needed one or two good positions to work on.

One more tweak was related to the fact that I didn’t want white’s probabilities to affect the probability of the paths, because I was playing white and could decide which path to take. For that reason I set all whites probabilities to 1.0 (a zero weight). The end result was a graph like this one:

Preparation

The position I settled on studying was this one:

According to Lichess this is an Alekhine defense (two pawn attack). In this position there’s only one good move for black (Nb6) and black is still at a slight disadvantage (+0.6 according to Stockfish). However, from that position PlayerX often plays Nf4, which is bad (+2.3). I created a study in Lichess and started looking at several variations (good moves and moves played by PlayerX). The end result was a tree of possibilities that I tried to memorize and understand. For example I needed to know what a move like d5 was threatening, why the move Nf4 was bad and prepare the best responses.

I didn’t spend much time doing this because I got bored pretty quickly, but I did prepare a bit for the upcoming match.

The match

As if I were predicting the future, in my match against PlayerX, we got into an Alekhine defense. Put under pressure he did end up blundering his knight at move 5. Turns out even players much better than you end up making one mistake after another when they are at a disadvantage. It’s easy to play accurately when you’re winning, but can you keep your cool when you are losing? At move 10 I was at a +7.1 advantage, pretty much impossible to lose, but I was also out of my preparation. Look at how cramped black’s position is and how my pieces are all pointing towards the enemy’s king:

I started making a bunch of mistakes from that point on, but I nevertheless was able to keep a non trivial advantage until move 27:

Unfortunately I was very low on time (it was a rapid 10 minutes game) and so I had to move quickly. I ended up messing up completely move 32 and 33, giving my half-dead opponent mate in one :/.

Here’s the full match (blunders and all):¹

Conclusion

What did I learn from this endeavour? A few things, most of which seem obvious in retrospect:

1. Preparing for a specific opponent can give a considerable edge in the opening.
2. Players at lower levels aren’t good at punishing dubious moves from the opponent. Getting into tricky positions where only one response is correct are easy ways to gain an advantage.
3. The opening isn’t everything. If you are bad at time management and tactics, it’s possible to lose completely winning positions. Chess games can be decided by one bad move.
4. Studying the game is important and there’s no silver bullet if your opponent is much better than you, but narrowing the skill gap is possible with specific preparation.
5. Applying software engineering principles to chess is fun. Doing it to have a chance at beating your brother is even more fun! I hope I’ll be able to do it one day :)

You can find the code I used in my GitHub repo. Note that I did not include the data and the code is quite messy, but I hope it can be of some inspiration, especially for folks that are considering whether computer science might be for them or not. Look, you can solve “real world” problems with it, it’s not just moving bits around!

That’s all folks, I hope I’ll be able to win a match against my brother some day, but until then, I’ll keep trying… my own way.

Feedback on Hacker News.